공부 기록
[WEEK 1] AI Math - 행렬 본문
▶ 행렬
- 벡터를 원소로 가지는 2차원 배열이다.
- $X = \begin{bmatrix}1&-2&3\\7&5&0\\-2&-1&2\end{bmatrix}$
x = np.array([[1, -2, 3],
[7, 5, 0],
[-2, -1, 2]])- 행백터를 원소로 가지는 2차원 배열로 이해하면 쉽다.
- $X = (x_{ij})$
- 행(row)과 열(column)이라는 인덱스를 가진다.
- 전치행렬 (transpose matrix)
- $X^T=(x_{ji})$
- 행과 열의 인덱스의 순서를 바꾼 행렬이다.
- NXM 행렬의 전치행렬은 MXN 행렬이 된다.
- 벡터에서도 성립된다.
▶ 행렬을 이해하는 방법(1)
- 행렬은 공간에서 여러 점들을 나타낸다.
- 데이터들의 모임이다.
- 행벡터 $\mathbf x_i$는 i번째 데이터를 의미한다.
- 행렬의 $x_{ij}$는 i 번째 데이터의 j 번째 변수의 값을 의미한다.
▶ 행렬의 덧셈, 뺄셈, 성분곱, 스칼라곱
- 행렬끼리 같은 모양을 가지면 덧셈, 뺄셈을 계산할 수 있다.
- 각 행렬의 구성 성분의 덧셈, 뺄셈으로 계산할 수 있다.
- 성분곱과 스칼라곱도 벡터와 같다.
▶ 행렬 곱셈
- $XY=\begin{pmatrix}\sum_kx_{ik}y_{kj}\end{pmatrix}$
- i번째 행벡터와 j번째 열벡터 사이의 내적을 성분으로 가지는 행렬을 계산한다.
- 행렬의 곱셈은 숫자의 곱셈과 달리 순서에 따라 계산결과가 달라진다.
- X의 열의 개수와 Y의 행의 개수가 같아야 연산이 가능하다.
import numpy as np
X = np.array([[1, -2, 3],
[7, 5, 0],
[-2, -1, 2]])
Y = np.array([[0, 1],
[1, -1],
[-2, 1]])
X @ Y
# array([[-8, 6],
# [ 5, 2],
# [-5, 1]])▶ 행렬 내적
- $XY^T=\begin{pmatrix}\sum_kx_{ik}y_{jk}\end{pmatrix}$
- np.inner는 i번째 행벡터와 j번째 행벡터 사이의 내적을 성분으로 가지는 행렬을 계산한다.
- np.inner와 수학에서의 내적은 개념이 다르다.
- 수학에서는 보통 $tr(XY^T)$을 내적으로 계산한다.
import numpy as np
X = np.array([[1, -2, 3],
[7, 5, 0],
[-2, -1, 2]])
Y = np.array([[0, 1, -1],
[1, -1, 0]])
np.inner(X, Y)
# array([[-5, 3],
# [ 5, 2],
# [-3, -1]])- 행렬곱에서는 X의 열의 갯수와 Y의 행의 갯수가 같아야 한다.
- np.inner에서는 X의 행의 갯수와 Y의 행의 갯수가 같아야 한다.
▶ 행렬을 이해하는 방법 2
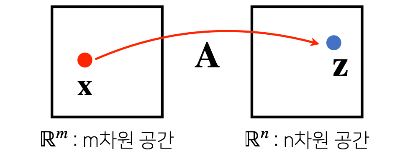
- $\mathbf Z=A\mathbf X$
- $z_i=\sum_ja_{ij}x_j$
- 행렬은 벡터공간에서 사용되는 연산자(operator)로 이해한다.
- 행렬을 통해 두 벡터를 연결지을 수 있다.
- 행렬곱을 통해 벡터를 다른 차원의 공간으로 보낼 수 있다.
- ex. m차원 공간 상에 존재하는 벡터를 n차원 공간으로 보냄
- 행렬곱을 통해 주어진 데이터에서 패턴을 추출할 수 있고, 데이터를 압축할 수 있다.
- 모든 선형변환 (linear transform)은 행렬곱으로 계산할 수 있다.
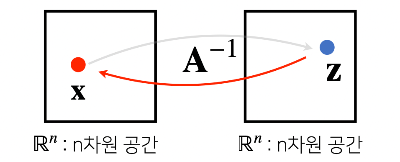
▶ 역행렬
- $A^{-1}$
- 행렬 $A$의 연산을 거꾸로 되돌리는 행렬을 역행렬(inverse matrix)이라고 한다.
- $AA^{-1}=A^{-1}A=I$
- 행과 열의 갯수가 같고 행렬식(determinant)이 0이 아닌 경우만 계산할 수 있다.
import numpy as np
X = np.array([[1, -2, 3],
[7, 5, 0],
[-2, -1, 2]])
np.linalg.inv(X) # 역행렬
# array([[ 0.21276596, 0.0212766 , -0.31914894],
# [-0.29787234, 0.17021277, 0.44680851],
# [ 0.06382979, 0.10638298, 0.40425532]])
X @ np.linalg.inv(X) # I
# array([[ 1.00000000e+00, 0.00000000e+00, 0.00000000e+00],
# [ 0.00000000e+00, 1.00000000e+00, 0.00000000e+00],
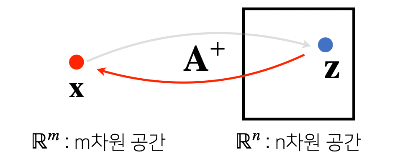
# [-5.55111512e-17, 0.00000000e+00, 1.00000000e+00]])▶ 유사역행렬(무어-펜로즈 역행렬)
- $A^+$
- 역행렬을 계산할 수 없을 때 대신 사용되는 개념이다.
- 행과 열의 갯수가 달라도 계산할 수 있다.
- $n\ge m$ 인 경우
- $A^+=(A^TA)^{-1}A^T$
- $A^+A=I$ (순서 중요!)
- $n\le m$ 인 경우
- $A^+=A^T(AA^T)^{-1}$
- $AA^+=I$ (순서 중요!)
import numpy as np
Y = np.array([[0, 1],
[1, -1],
[-2, 1]])
np.linalg.pinv(Y)
# array([[ 5.00000000e-01, 1.11022302e-16, -5.00000000e-01],
# [ 8.33333333e-01, -3.33333333e-01, -1.66666667e-01]])
np.linalg.pinv(Y) @ Y
# array([[ 1.00000000e+00, -2.22044605e-16],
# [ 1.11022302e-16, 1.00000000e+00]])▶ 응용 1 : 연립방정식
- np.linalg.pinv를 이용하면 연립방정식의 해를 구할 수 있다.
- $n \le m$ 인 경우 : 식이 변수 개수보다 작거나 같아야 한다.
- $A\mathbf x=\mathbf b$
- $\mathbf x=A^+\mathbf b=A^T(AA^T)^{-1}\mathbf b$
▶ 응용 2 : 선형 회귀 분석
- np.linalg.pinv를 이용하면 데이터를 선형 모델로 해석하는 선형회귀식을 찾을 수 있다.
- $n\ge m$ 인 경우 : 데이터가 변수 개수보다 많거나 같아야 한다.
- 선형회귀분석은 연립방정식과 달리 행이 더 크므로 방정식을 푸는 건 불가능하고 주어진 데이터를 가장 잘 표현할 수 있는 선을 찾는 것이 최선이다.
- $X\beta=\mathbf {\hat y}\approx\mathbf y$
- $\beta = X^+\mathbf y=(X^TX)^{-1}X^T\mathbf y$ (L2-노름을 최소화하는 계수 $\beta$)
- sklearn의 LinearRegression과 같은 결과를 가져올 수 있다.
※ 모든 시각 자료는 부스트 캠프 AI Tech 교육 자료를 참고했습니다.
'BOOST CAMP - AI Tech' 카테고리의 다른 글
| [WEEK 1] AI Math - 딥러닝 학습 방법 (0) | 2022.09.25 |
|---|---|
| [WEEK 1] AI Math - 경사하강법 (0) | 2022.09.25 |
| [WEEK 1] AI Math - 벡터 (0) | 2022.09.25 |
| [WEEK 1] Object-Oriented Programming (0) | 2022.09.23 |
| [WEEK 1] Pythonic code (2) | 2022.09.23 |
Comments



